scale_matrix Module Reference

module MATRIX More...

Functions/Subroutines
subroutine, public	matrix_setup
	Setup. More...
subroutine, public	matrix_finalize
	Finalize. More...
subroutine, public	matrix_solver_tridiagonal_1d_ta ( KA, KS, KE, ifdef _OPENACC
	solve tridiagonal matrix with Thomas's algorithm More...
subroutine, public	matrix_solver_tridiagonal_1d_cr ( KA, KS, KE, ifdef _OPENACC
	solve tridiagonal matrix with Cyclic Reduction method More...
subroutine, public	matrix_solver_tridiagonal_1d_pcr ( KA, KS, KE, ifdef _OPENACC
	solve tridiagonal matrix with Parallel Cyclic Reduction method More...
subroutine	matrix_solver_tridiagonal_2d_block (KA, KS, KE, ud, md, ld, iv, ov)
subroutine, public	matrix_solver_eigenvalue_decomposition (n, a, eival, eivec, simdlen)

Detailed Description

module MATRIX

Description

solve matrix module

Author

Team SCALE

Function/Subroutine Documentation

matrix_setup()

subroutine, public scale_matrix::matrix_setup

Setup.

Definition at line 80 of file scale_matrix.F90.

    use scale_prc, only: &
       prc_abort
    implicit none
 
!    namelist /PARAM_MATRIX/ &
 
    integer :: ierr
    !---------------------------------------------------------------------------
 
    log_newline
    log_info("MATRIX_setup",*) 'Setup'
 
    !--- read namelist
!!$    rewind(IO_FID_CONF)
!!$    read(IO_FID_CONF,nml=PARAM_MATRIX,iostat=ierr)
!!$    if( ierr < 0 ) then !--- missing
!!$       LOG_INFO("MATRIX_setup",*) 'Not found namelist. Default used.'
!!$    elseif( ierr > 0 ) then !--- fatal error
!!$       LOG_ERROR("MATRIX_setup",*) 'Not appropriate names in namelist PARAM_MATRIX. Check!'
!!$       call PRC_abort
!!$    endif
!!$    LOG_NML(PARAM_MATRIX)
 
#ifdef USE_CUDALIB
    status = cusparsecreate(handle)
    if ( status /= cusparse_status_success ) then
       log_error("MATRIX_setup",*) "cusparseCreate failed: ", status
       call prc_abort
    end if
    bufsize = -1
#endif
    return

References scale_prc::prc_abort().

Referenced by mod_rm_driver::rm_driver().

Here is the call graph for this function:

Here is the caller graph for this function:

matrix_finalize()

subroutine, public scale_matrix::matrix_finalize

Finalize.

Definition at line 117 of file scale_matrix.F90.

 
#ifdef USE_CUDALIB
    status = cusparsedestroy(handle)
    if ( allocated(pbuffer) ) deallocate(pbuffer)
    bufsize = -1
#endif
 
    return

Referenced by mod_rm_driver::rm_driver().

Here is the caller graph for this function:

matrix_solver_tridiagonal_1d_ta()

subroutine, public scale_matrix::matrix_solver_tridiagonal_1d_ta	(	integer, intent(in)	KA,
		integer, intent(in)	KS,
		integer, intent(in)	KE,
			ifdef,
			_OPENACC
	)

solve tridiagonal matrix with Thomas's algorithm

Definition at line 133 of file scale_matrix.F90.

       work,       &
#endif
       ud, md, ld, &
       iv,         &
       ov          )
    !$acc routine seq
    implicit none
    integer,  intent(in)  :: KA, KS, KE
 
    real(RP), intent(in)  :: ud(KA) ! upper  diagonal
    real(RP), intent(in)  :: md(KA) ! middle diagonal
    real(RP), intent(in)  :: ld(KA) ! lower  diagonal
    real(RP), intent(in)  :: iv(KA) ! input  vector
 
    real(RP), intent(out) :: ov(KA) ! output vector
 
#ifdef _OPENACC
    real(RP), intent(out) :: work(KS:KE,2)
#define c_ta(k) work(k,1)
#define d_ta(k) work(k,2)
#else
    real(RP) :: c_ta(KS:KE)
    real(RP) :: d_ta(KS:KE)
#endif
    real(RP) :: rdenom
 
    integer :: k
    !---------------------------------------------------------------------------
 
    ! foward reduction
    c_ta(ks) = ud(ks) / md(ks)
    d_ta(ks) = iv(ks) / md(ks)
    do k = ks+1, ke-1
       rdenom = 1.0_rp / ( md(k) - ld(k) * c_ta(k-1) )
       c_ta(k) =           ud(k)               * rdenom
       d_ta(k) = ( iv(k) - ld(k) * d_ta(k-1) ) * rdenom
    enddo
 
    ! backward substitution
    ov(ke) = ( iv(ke) - ld(ke) * d_ta(ke-1) ) / ( md(ke) - ld(ke) * c_ta(ke-1) )
    do k = ke-1, ks, -1
       ov(k) = d_ta(k) - c_ta(k) * ov(k+1)
    enddo
 
    return

Referenced by scale_interp::cross().

Here is the caller graph for this function:

matrix_solver_tridiagonal_1d_cr()

subroutine, public scale_matrix::matrix_solver_tridiagonal_1d_cr	(	integer, intent(in)	KA,
		integer, intent(in)	KS,
		integer, intent(in)	KE,
			ifdef,
			_OPENACC
	)

solve tridiagonal matrix with Cyclic Reduction method

Definition at line 186 of file scale_matrix.F90.

       work,       &
#endif
       ud, md, ld, &
       iv,         &
       ov          )
    !$acc routine vector
    implicit none
    integer,  intent(in)  :: KA, KS, KE
 
    real(RP), intent(in)  :: ud(KA) ! upper  diagonal
    real(RP), intent(in)  :: md(KA) ! middle diagonal
    real(RP), intent(in)  :: ld(KA) ! lower  diagonal
    real(RP), intent(in)  :: iv(KA) ! input  vector
 
    real(RP), intent(out) :: ov(KA) ! output vector
 
#ifdef _OPENACC
    real(RP), intent(out) :: work(KE-KS+1,4)
#define a1_cr(k) work(k,1)
#define b1_cr(k) work(k,2)
#define c1_cr(k) work(k,3)
#define x1_cr(k) work(k,4)
#else
    real(RP) :: a1_cr(KE-KS+1)
    real(RP) :: b1_cr(KE-KS+1)
    real(RP) :: c1_cr(KE-KS+1)
    real(RP) :: x1_cr(KE-KS+1)
#endif
    real(RP) :: f1, f2
    integer :: st
    integer :: lmax, kmax
    integer :: k, k1, k2, l
 
    kmax = ke - ks + 1
    lmax = floor( log(real(kmax,rp)) / log(2.0_rp) ) - 1
 
    a1_cr(:) = ld(ks:ke)
    b1_cr(:) = md(ks:ke)
    c1_cr(:) = ud(ks:ke)
    x1_cr(:) = iv(ks:ke)
 
    st = 1
    do l = 1, lmax
       !$omp parallel do private(k1,k2,f1,f2)
       !$acc loop private(k1,k2,f1,f2)
       do k = st*2, kmax, st*2
          k1 = k - st
          k2 = k + st
          f1 = a1_cr(k) / b1_cr(k1)
          if ( k2 > kmax ) then
             k2 = k1 ! dummy
             f2 = 0.0_rp
          else
             f2 = c1_cr(k) / b1_cr(k2)
          end if
          a1_cr(k) = - a1_cr(k1) * f1
          c1_cr(k) = - c1_cr(k2) * f2
          b1_cr(k) = b1_cr(k) - c1_cr(k1) * f1 - a1_cr(k2) * f2
          x1_cr(k) = x1_cr(k) - x1_cr(k1) * f1 - x1_cr(k2) * f2
       end do
       st = st * 2
    end do
    if ( kmax / st == 2 ) then
       ov(ks+st*2-1) = ( a1_cr(st*2) * x1_cr(st) - b1_cr(st) * x1_cr(st*2) ) &
               / ( a1_cr(st*2) * c1_cr(st) - b1_cr(st) * b1_cr(st*2) )
       ov(ks+st-1) = ( x1_cr(st) - c1_cr(st) * ov(ks+st*2-1) ) / b1_cr(st)
    else if ( kmax / st == 3 ) then
       k = st * 2
       k1 = st * 2 - st
       k2 = st * 2 + st
       f2 = c1_cr(k1) / b1_cr(k)
       c1_cr(k1) = - c1_cr(k) * f2
       b1_cr(k1) = b1_cr(k1) - a1_cr(k) * f2
       x1_cr(k1) = x1_cr(k1) - x1_cr(k) * f2
 
       f1 = a1_cr(k2) / b1_cr(k)
       a1_cr(k2) = - a1_cr(k) * f1
       b1_cr(k2) = b1_cr(k2) - c1_cr(k) * f1
       x1_cr(k2) = x1_cr(k2) - x1_cr(k) * f1
 
       ov(ks+k2-1) = ( a1_cr(k2) * x1_cr(k1) - b1_cr(k1) * x1_cr(k2) ) &
              / ( a1_cr(k2) * c1_cr(k1) - b1_cr(k1) * b1_cr(k2) )
       ov(ks+k1-1) = ( x1_cr(k1) - c1_cr(k1) * ov(ks+k2-1) ) / b1_cr(k1)
       ov(ks+k-1) = ( x1_cr(k) - a1_cr(k) * ov(ks+k1-1) - c1_cr(k) * ov(ks+k2-1) ) / b1_cr(k)
    end if
 
    do l = 1, lmax
       st = st / 2
       !$omp parallel do
       !$acc loop independent
       do k = st, kmax, st*2
          if ( k-st < 1 ) then
             ov(ks+k-1) = ( x1_cr(k) - c1_cr(k) * ov(ks+k+st-1) ) / b1_cr(k)
          elseif ( k+st <= kmax ) then
             ov(ks+k-1) = ( x1_cr(k) - a1_cr(k) * ov(ks+k-st-1) - c1_cr(k) * ov(ks+k+st-1) ) / b1_cr(k)
          else
             ov(ks+k-1) = ( x1_cr(k) - a1_cr(k) * ov(ks+k-st-1) ) / b1_cr(k)
          end if
       end do
    end do
 
    return

Referenced by scale_atmos_dyn_tstep_short_fvm_hevi::atmos_dyn_tstep_short_fvm_hevi(), scale_land_dyn_bucket::land_dyn_bucket(), matrix_solver_tridiagonal_1d_pcr(), and matrix_solver_tridiagonal_2d_block().

Here is the caller graph for this function:

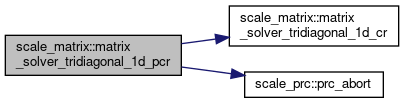
matrix_solver_tridiagonal_1d_pcr()

subroutine, public scale_matrix::matrix_solver_tridiagonal_1d_pcr	(	integer, intent(in)	KA,
		integer, intent(in)	KS,
		integer, intent(in)	KE,
			ifdef,
			_OPENACC
	)

solve tridiagonal matrix with Parallel Cyclic Reduction method

Definition at line 296 of file scale_matrix.F90.

       work,       &
#endif
       ud, md, ld, &
       iv,         &
       ov          )
    !$acc routine vector
    implicit none
    integer,  intent(in)  :: KA, KS, KE
 
    real(RP), intent(in)  :: ud(KA) ! upper  diagonal
    real(RP), intent(in)  :: md(KA) ! middle diagonal
    real(RP), intent(in)  :: ld(KA) ! lower  diagonal
    real(RP), intent(in)  :: iv(KA) ! input  vector
 
    real(RP), intent(out) :: ov(KA) ! output vector
 
#ifdef _OPENACC
    real(RP), intent(out) :: work(KE-KS+1,2,4)
#define a1_pcr(k,n) work(k,n,1)
#define b1_pcr(k,n) work(k,n,2)
#define c1_pcr(k,n) work(k,n,3)
#define x1_pcr(k,n) work(k,n,4)
#else
    real(RP) :: a1_pcr(KE-KS+1,2)
    real(RP) :: b1_pcr(KE-KS+1,2)
    real(RP) :: c1_pcr(KE-KS+1,2)
    real(RP) :: x1_pcr(KE-KS+1,2)
#endif
    real(RP) :: f1, f2
    integer :: st
    integer :: lmax, kmax
    integer :: iw1, iw2, iws
    integer :: k, k1, k2, l
 
    kmax = ke - ks + 1
    lmax = ceiling( log(real(kmax,rp)) / log(2.0_rp) )
 
    a1_pcr(:,1) = ld(ks:ke)
    b1_pcr(:,1) = md(ks:ke)
    c1_pcr(:,1) = ud(ks:ke)
    x1_pcr(:,1) = iv(ks:ke)
 
    st = 1
    iw1 = 1
    iw2 = 2
    do l = 1, lmax
       !$omp parallel do private(k1,k2,f1,f2)
       !$acc loop private(k1,k2,f1,f2)
       do k = 1, kmax
          k1 = k - st
          k2 = k + st
          if ( k1 < 1 ) then
             k1 = k ! dummy
             f1 = 0.0_rp
          else
             f1 = a1_pcr(k,iw1) / b1_pcr(k1,iw1)
          end if
          if ( k2 > kmax ) then
             k2 = k ! dummy
             f2 = 0.0_rp
          else
             f2 = c1_pcr(k,iw1) / b1_pcr(k2,iw1)
          end if
          a1_pcr(k,iw2) = - a1_pcr(k1,iw1) * f1
          c1_pcr(k,iw2) = - c1_pcr(k2,iw1) * f2
          b1_pcr(k,iw2) = b1_pcr(k,iw1) - c1_pcr(k1,iw1) * f1 - a1_pcr(k2,iw1) * f2
          x1_pcr(k,iw2) = x1_pcr(k,iw1) - x1_pcr(k1,iw1) * f1 - x1_pcr(k2,iw1) * f2
       end do
       st = st * 2
       iws = iw2
       iw2 = iw1
       iw1 = iws
    end do
 
    !$omp parallel do
    do k = 1, kmax
       ov(ks+k-1) = x1_pcr(k,iw1) / b1_pcr(k,iw1)
    end do
 
    return

References matrix_solver_tridiagonal_1d_cr(), and scale_prc::prc_abort().

Here is the call graph for this function:

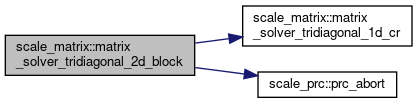
matrix_solver_tridiagonal_2d_block()

subroutine scale_matrix::matrix_solver_tridiagonal_2d_block	(	integer, intent(in)	KA,
		integer, intent(in)	KS,
		integer, intent(in)	KE,
		real(rp), dimension(ka,lsize), intent(in)	ud,
		real(rp), dimension(ka,lsize), intent(in)	md,
		real(rp), dimension(ka,lsize), intent(in)	ld,
		real(rp), dimension(ka,lsize), intent(in)	iv,
		real(rp), dimension(ka,lsize), intent(out)	ov
	)

Definition at line 536 of file scale_matrix.F90.

    !$acc routine vector
    implicit none
    integer,  intent(in)  :: KA, KS, KE
 
    real(RP), intent(in)  :: ud(KA,LSIZE) ! upper  diagonal
    real(RP), intent(in)  :: md(KA,LSIZE) ! middle diagonal
    real(RP), intent(in)  :: ld(KA,LSIZE) ! lower  diagonal
    real(RP), intent(in)  :: iv(KA,LSIZE) ! input  vector
 
    real(RP), intent(out) :: ov(KA,LSIZE) ! output vector
 
    real(RP) :: c(LSIZE,KS:KE)
    real(RP) :: d(LSIZE,KS:KE)
    real(RP) :: work(LSIZE,KS:KE)
    real(RP) :: rdenom
 
    integer :: k, l
    !---------------------------------------------------------------------------
 
    ! foward reduction
    do l = 1, lsize
       c(l,ks) = ud(ks,l) / md(ks,l)
       d(l,ks) = iv(ks,l) / md(ks,l)
    end do
    do k = ks+1, ke-1
!OCL NOFULLUNROLL_PRE_SIMD
       do l = 1, lsize
          rdenom = 1.0_rp / ( md(k,l) - ld(k,l) * c(l,k-1) )
          c(l,k) =            ud(k,l)              * rdenom
          d(l,k) = ( iv(k,l) - ld(k,l) * d(l,k-1) ) * rdenom
       end do
    end do
 
    ! backward substitution
    do l = 1, lsize
       work(l,ke) = ( iv(ke,l) - ld(ke,l) * d(l,ke-1) ) / ( md(ke,l) - ld(ke,l) * c(l,ke-1) )
    end do
    do k = ke-1, ks, -1
!OCL NOFULLUNROLL_PRE_SIMD
       do l = 1, lsize
          work(l,k) = d(l,k) - c(l,k) * work(l,k+1)
       end do
    end do
 
    do l = 1, lsize
    do k = ks, ke
       ov(k,l) = work(l,k)
    end do
    end do
 
    return

References matrix_solver_tridiagonal_1d_cr(), and scale_prc::prc_abort().

Here is the call graph for this function:

matrix_solver_eigenvalue_decomposition()

subroutine, public scale_matrix::matrix_solver_eigenvalue_decomposition	(	integer, intent(in)	n,
		real(rp), dimension (n,n), intent(in)	a,
		real(rp), dimension(n), intent(out)	eival,
		real(rp), dimension(n,n), intent(out)	eivec,
		integer, intent(in), optional	simdlen
	)

Definition at line 879 of file scale_matrix.F90.

    use scale_prc, only: &
      prc_abort
    implicit none
 
    integer,  intent(in)  :: n            ! dimension of matrix
    real(RP), intent(in)  :: a    (n,n)   ! input matrix
    real(RP), intent(out) :: eival(n)     ! eiven values in decending order. i.e. eival(1) is the largest
    real(RP), intent(out) :: eivec(n,n)   ! eiven vectors
 
    integer, intent(in), optional :: simdlen
 
    real(RP) :: eival_inc
 
    real(RP), allocatable :: b    (:,:)
    real(RP), allocatable :: w    (:)
    real(RP), allocatable :: work (:)     ! working array, size is lwork  = 2*n*n + 6*n + 1
    integer,  allocatable :: iwork(:)     ! working array, size is liwork = 5*n + 3
 
    integer :: simdlen_
    integer :: nrank_eff
    integer :: lda
    integer :: lwork
    integer :: liwork
 
    integer :: iblk, jblk
    integer :: imax, jmax
    integer :: ivec, jvec
 
    integer :: i, j, ierr
    !---------------------------------------------------------------------------
 
#ifdef DA
    if( present(simdlen) ) then
      simdlen_ = simdlen
    else
      simdlen_ = 64
    end if
 
    lda = n
 
    lwork  = 2*n*n + 6*n + 1
    liwork = 5*n + 3
 
    allocate( b(lda,n)  )
    allocate( w(lda)    )
    allocate( work(lwork)  )
    allocate( iwork(liwork) )
 
    do jblk = 1, n, simdlen_
       jmax = min( n-jblk+1, simdlen_ )
       do iblk = 1, n, simdlen_
          imax = min( n-iblk+1, simdlen_ )
 
          do jvec = 1, jmax
             j = jblk + jvec - 1
             do ivec = 1, imax
                i = iblk + ivec - 1
 
                b(i,j) = 0.5_rp * ( a(i,j) + a(j,i) )
             end do
          end do
       end do
    end do
 
    ! use the SSYEVD/DSYEVD subroutine in LAPACK
    if( rp == sp ) then
       call ssyevd("V","L",n,b,lda,w,work,lwork,iwork,liwork,ierr)
    else
       call dsyevd("V","L",n,b,lda,w,work,lwork,iwork,liwork,ierr)
    end if
 
    if( ierr /= 0 ) then
       log_info('MATRIX_SOLVER_eigenvalue_decomposition',*) 'LAPACK/SYEVD error code is ', ierr
       log_info('MATRIX_SOLVER_eigenvalue_decomposition',*) 'input a'
       do j = 1, n
          log_info('MATRIX_SOLVER_eigenvalue_decomposition',*) j ,a(:,j)
       enddo
       log_info('MATRIX_SOLVER_eigenvalue_decomposition',*) 'output eival'
       log_info('MATRIX_SOLVER_eigenvalue_decomposition',*) w(:)
       log_info('MATRIX_SOLVER_eigenvalue_decomposition',*) 'output eivec'
       do j = 1, n
          log_info('MATRIX_SOLVER_eigenvalue_decomposition',*) j, b(:,j)
       enddo
       log_info('MATRIX_SOLVER_eigenvalue_decomposition',*) 'Try to use LAPACK/SYEV ...'
 
       ! Temporary treatment because of the instability of SYEVD
       do jblk = 1, n, simdlen_
          jmax = min( n-jblk+1, simdlen_ )
          do iblk = 1, n, simdlen_
             imax = min( n-iblk+1, simdlen_ )
 
             do jvec = 1, jmax
                j = jblk + jvec - 1
                do ivec = 1, imax
                   i = iblk + ivec - 1
 
                   b(i,j) = 0.5_rp * ( a(i,j) + a(j,i) )
                end do
             end do
          end do
       end do
 
       ! use SSYEV/DSYEV subroutine in LAPACK
       if( rp == sp ) then
          call ssyev("V","L",n,b,lda,w,work,lwork,ierr)
       else
          call dsyev("V","L",n,b,lda,w,work,lwork,ierr)
       end if
 
       if ( ierr /= 0 ) then
          log_error('MATRIX_SOLVER_eigenvalue_decomposition',*) 'LAPACK/SYEV error code is ', ierr, '! STOP.'
          call prc_abort
       endif
    endif
 
    if( w(1) < 0.0_rp ) then
       eival_inc = w(n) / ( 1.e+5_rp - 1.0_rp )
       do i = 1, n
          w(i) = w(i) + eival_inc
       enddo
    else if( w(n)/1.e+5_rp > w(1) ) then
       eival_inc = ( w(n) - w(1)*1.e+5_rp ) / ( 1.e+5_rp - 1.0_rp )
       do i = 1, n
          w(i) = w(i) + eival_inc
       end do
    end if
 
    ! reverse order
    do i = 1, n
       eival(i) = w(i)
    enddo
    do j = 1, n
    do i = 1, n
       eivec(i,j) = b(i,j)
    enddo
    enddo
 
    nrank_eff = n
 
    if( eival(n) > 0.0_rp ) then
       do i = 1, n
          if( eival(i) < abs(eival(n))*sqrt(epsilon(eival)) ) then
             nrank_eff = nrank_eff - 1
             eival(i) = 0.0_rp
             eivec(:,i) = 0.0_rp
          end if
       end do
    else
       ! check zero
       log_error('MATRIX_SOLVER_eigenvalue_decomposition',*) 'All eigenvalues are below 0! STOP.'
       call prc_abort
    endif
 
    deallocate( b )
    deallocate( w )
    deallocate( work )
    deallocate( iwork )
#else
    log_error('MATRIX_SOLVER_eigenvalue_decomposition',*) 'Binary not compiled for DA! STOP.'
    call prc_abort
#endif
 
    return

References scale_prc::prc_abort(), and scale_precision::sp.

Referenced by scale_letkf::letkf_add_inflation_setup(), and scale_letkf::letkf_system().

Here is the call graph for this function:

Here is the caller graph for this function: