SCALE-RM
Functions/Subroutines
scale_vector Module Reference

module vector More...

Functions/Subroutines

subroutine, public vectr_xyz2latlon (x, y, z, lat, lon)
 
subroutine, public vectr_latlon2xyz (lat, lon, x, y, z, radius)
 
subroutine, public vectr_cross (nv, a, b, c, d)
 exterior product of vector a->b and c->d More...
 
subroutine, public vectr_dot (l, a, b, c, d)
 interior product of vector a->b and c->d More...
 
subroutine, public vectr_abs (l, a)
 length of vector o->a More...
 
subroutine, public vectr_angle (angle, a, b, c)
 calc angle between two vector(b->a,b->c) More...
 
subroutine, public vectr_intersec (ifcross, p, a, b, c, d)
 judge intersection of two vector More...
 
subroutine, public vectr_anticlockwise (vertex, nvert)
 bubble sort anticlockwise by angle More...
 
real(rp) function, public vectr_triangle (a, b, c, polygon_type, radius)
 
subroutine, public vectr_distance (r, lon1, lat1, lon2, lat2, dist)
 Get horizontal distance on the sphere. More...
 

Detailed Description

module vector

Description
module for 3D vector on the sphere
Author
NICAM developers, Team SCALE

Function/Subroutine Documentation

◆ vectr_xyz2latlon()

subroutine, public scale_vector::vectr_xyz2latlon ( real(rp), intent(in)  x,
real(rp), intent(in)  y,
real(rp), intent(in)  z,
real(rp), intent(out)  lat,
real(rp), intent(out)  lon 
)

Definition at line 57 of file scale_vector.F90.

References scale_const::const_eps.

57  use scale_const, only: &
58  const_eps
59  implicit none
60 
61  real(RP),intent(in) :: x
62  real(RP),intent(in) :: y
63  real(RP),intent(in) :: z
64  real(RP),intent(out) :: lat
65  real(RP),intent(out) :: lon
66 
67  real(RP) :: length, length_h
68  !---------------------------------------------------------------------------
69 
70  length = sqrt( x*x + y*y + z*z )
71 
72  if ( length < const_eps ) then ! 3D vector length is
73  lat = 0.0_rp
74  lon = 0.0_rp
75  return
76  endif
77 
78  if ( z / length >= 1.0_rp ) then ! vector is parallele to z axis.
79  lat = asin(1.0_rp)
80  lon = 0.0_rp
81  return
82  elseif( z / length <= -1.0_rp ) then ! vector is parallele to z axis.
83  lat = asin(-1.0_rp)
84  lon = 0.0_rp
85  return
86  else
87  lat = asin( z / length )
88  endif
89 
90  length_h = sqrt( x*x + y*y )
91 
92  if ( length_h < const_eps ) then
93  lon = 0.0_rp
94  return
95  endif
96 
97  if ( x / length_h >= 1.0_rp ) then
98  lon = acos(1.0_rp)
99  elseif( x / length_h <= -1.0_rp ) then
100  lon = acos(-1.0_rp)
101  else
102  lon = acos( x / length_h )
103  endif
104 
105  if( y < 0.0_rp ) lon = -lon
106 
107  return
scale_const
module CONSTANT
Definition: scale_const.F90:14
scale_const::const_eps
real(rp), public const_eps
small number
Definition: scale_const.F90:36

◆ vectr_latlon2xyz()

subroutine, public scale_vector::vectr_latlon2xyz ( real(rp), intent(in)  lat,
real(rp), intent(in)  lon,
real(rp), intent(out)  x,
real(rp), intent(out)  y,
real(rp), intent(out)  z,
real(rp), intent(in)  radius 
)

Definition at line 118 of file scale_vector.F90.

118  implicit none
119 
120  real(RP),intent(in) :: lat
121  real(RP),intent(in) :: lon
122  real(RP),intent(out) :: x
123  real(RP),intent(out) :: y
124  real(RP),intent(out) :: z
125  real(RP),intent(in) :: radius
126  !---------------------------------------------------------------------------
127 
128  x = radius * cos(lat) * cos(lon)
129  y = radius * cos(lat) * sin(lon)
130  z = radius * sin(lat)
131 
132  return

◆ vectr_cross()

subroutine, public scale_vector::vectr_cross ( real(rp), dimension(3), intent(out)  nv,
real(rp), dimension(3), intent(in)  a,
real(rp), dimension(3), intent(in)  b,
real(rp), dimension(3), intent(in)  c,
real(rp), dimension(3), intent(in)  d 
)

exterior product of vector a->b and c->d

Definition at line 138 of file scale_vector.F90.

Referenced by vectr_angle(), vectr_anticlockwise(), vectr_intersec(), and vectr_triangle().

138  implicit none
139 
140  real(RP), intent(out) :: nv(3) ! normal vector
141  real(RP), intent(in ) :: a(3), b(3), c(3), d(3) ! x,y,z(cartesian)
142  !---------------------------------------------------------------------------
143 
144  nv(1) = ( b(2)-a(2) ) * ( d(3)-c(3) ) &
145  - ( b(3)-a(3) ) * ( d(2)-c(2) )
146  nv(2) = ( b(3)-a(3) ) * ( d(1)-c(1) ) &
147  - ( b(1)-a(1) ) * ( d(3)-c(3) )
148  nv(3) = ( b(1)-a(1) ) * ( d(2)-c(2) ) &
149  - ( b(2)-a(2) ) * ( d(1)-c(1) )
150 
151  return
Here is the caller graph for this function:

◆ vectr_dot()

subroutine, public scale_vector::vectr_dot ( real(rp), intent(out)  l,
real(rp), dimension(3), intent(in)  a,
real(rp), dimension(3), intent(in)  b,
real(rp), dimension(3), intent(in)  c,
real(rp), dimension(3), intent(in)  d 
)

interior product of vector a->b and c->d

Definition at line 157 of file scale_vector.F90.

Referenced by vectr_angle(), vectr_anticlockwise(), and vectr_intersec().

157  implicit none
158 
159  real(RP), intent(out) :: l
160  real(RP), intent(in ) :: a(3), b(3), c(3), d(3) ! x,y,z(cartesian)
161  !---------------------------------------------------------------------------
162  ! if a=c=zero-vector and b=d, result is abs|a|^2
163 
164  l = ( b(1)-a(1) ) * ( d(1)-c(1) ) &
165  + ( b(2)-a(2) ) * ( d(2)-c(2) ) &
166  + ( b(3)-a(3) ) * ( d(3)-c(3) )
167 
168  return
Here is the caller graph for this function:

◆ vectr_abs()

subroutine, public scale_vector::vectr_abs ( real(rp), intent(out)  l,
real(rp), dimension(3), intent(in)  a 
)

length of vector o->a

Definition at line 174 of file scale_vector.F90.

Referenced by vectr_angle(), vectr_intersec(), and vectr_triangle().

174  implicit none
175 
176  real(RP), intent(out) :: l
177  real(RP), intent(in ) :: a(3) ! x,y,z(cartesian)
178  !---------------------------------------------------------------------------
179 
180  l = a(1)*a(1) + a(2)*a(2) + a(3)*a(3)
181  l = sqrt(l)
182 
183  return
Here is the caller graph for this function:

◆ vectr_angle()

subroutine, public scale_vector::vectr_angle ( real(rp), intent(out)  angle,
real(rp), dimension(3), intent(in)  a,
real(rp), dimension(3), intent(in)  b,
real(rp), dimension(3), intent(in)  c 
)

calc angle between two vector(b->a,b->c)

Definition at line 189 of file scale_vector.F90.

References vectr_abs(), vectr_cross(), and vectr_dot().

Referenced by vectr_anticlockwise(), vectr_intersec(), and vectr_triangle().

189  implicit none
190 
191  real(RP), intent(out) :: angle
192  real(RP), intent(in ) :: a(3), b(3), c(3)
193 
194  real(RP) :: nv(3), nvlens, nvlenc
195  !---------------------------------------------------------------------
196 
197  call vectr_dot ( nvlenc, b, a, b, c )
198  call vectr_cross( nv(:), b, a, b, c )
199  call vectr_abs ( nvlens, nv(:) )
200  angle = atan2( nvlens, nvlenc )
201 
202  return
Here is the call graph for this function:
Here is the caller graph for this function:

◆ vectr_intersec()

subroutine, public scale_vector::vectr_intersec ( logical, intent(out)  ifcross,
real(rp), dimension(3), intent(out)  p,
real(rp), dimension(3), intent(in)  a,
real(rp), dimension(3), intent(in)  b,
real(rp), dimension(3), intent(in)  c,
real(rp), dimension(3), intent(in)  d 
)

judge intersection of two vector

Definition at line 208 of file scale_vector.F90.

References vectr_abs(), vectr_angle(), vectr_cross(), and vectr_dot().

208  implicit none
209 
210  logical, intent(out) :: ifcross
211  ! .true. : line a->b and c->d intersect
212  ! .false.: line a->b and c->d do not intersect and p = (0,0)
213  real(RP), intent(out) :: p(3) ! intersection point
214  real(RP), intent(in ) :: a(3), b(3), c(3), d(3)
215 
216  real(RP), parameter :: o(3) = 0.0_rp
217 
218  real(RP) :: oaob(3), ocod(3), cdab(3)
219  real(RP) :: ip, length
220  real(RP) :: angle_aop, angle_pob, angle_aob
221  real(RP) :: angle_cop, angle_pod, angle_cod
222 
223  real(RP), parameter :: eps = 1.e-12_rp
224  !---------------------------------------------------------------------
225 
226  call vectr_cross( oaob, o, a, o, b )
227  call vectr_cross( ocod, o, c, o, d )
228  call vectr_cross( cdab, o, ocod, o, oaob )
229 
230  call vectr_abs ( length, cdab )
231  call vectr_dot ( ip, o, cdab, o, a )
232 
233  p(:) = cdab(:) / sign(length,ip)
234 ! write(ADM_LOG_FID,*), "p:", p(:)
235 
236  call vectr_angle( angle_aop, a, o, p )
237  call vectr_angle( angle_pob, p, o, b )
238  call vectr_angle( angle_aob, a, o, b )
239 ! write(ADM_LOG_FID,*), "angle a-p-b:", angle_aop, angle_pob, angle_aob
240 
241  call vectr_angle( angle_cop, c, o, p )
242  call vectr_angle( angle_pod, p, o, d )
243  call vectr_angle( angle_cod, c, o, d )
244 ! write(ADM_LOG_FID,*), "angle c-p-d:", angle_cop, angle_pod, angle_cod
245 
246 ! write(ADM_LOG_FID,*), "judge:", angle_aob-(angle_aop+angle_pob), angle_cod-(angle_cop+angle_pod)
247 
248  ! --- judge intersection
249  if ( abs(angle_aob-(angle_aop+angle_pob)) < eps &
250  .AND. abs(angle_cod-(angle_cop+angle_pod)) < eps &
251  .AND. abs(angle_aop) > eps &
252  .AND. abs(angle_pob) > eps &
253  .AND. abs(angle_cop) > eps &
254  .AND. abs(angle_pod) > eps ) then
255  ifcross = .true.
256  else
257  ifcross = .false.
258  p(:) = 0.0_rp
259  endif
260 
261  return
Here is the call graph for this function:

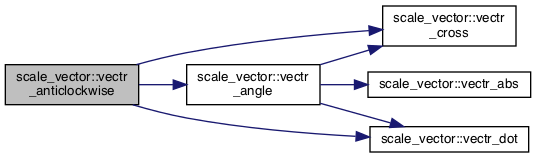
◆ vectr_anticlockwise()

subroutine, public scale_vector::vectr_anticlockwise ( real(rp), dimension(nvert,3), intent(inout)  vertex,
integer, intent(in)  nvert 
)

bubble sort anticlockwise by angle

Definition at line 267 of file scale_vector.F90.

References vectr_angle(), vectr_cross(), and vectr_dot().

267  implicit none
268 
269  integer, intent(in) :: nvert
270  real(RP), intent(inout) :: vertex(nvert,3)
271 
272  real(RP), parameter :: o(3) = 0.0_rp
273  real(RP) :: v1(3), v2(3), v3(3)
274  real(RP) :: xp(3), ip
275  real(RP) :: angle1, angle2
276 
277  real(RP), parameter :: eps = 1.e-12_rp
278 
279  integer :: i, j
280  !---------------------------------------------------------------------
281 
282  do j = 2 , nvert-1
283  do i = j+1, nvert
284  v1(:) = vertex(1,:)
285  v2(:) = vertex(j,:)
286  v3(:) = vertex(i,:)
287 
288  call vectr_cross( xp(:), v1(:), v2(:), v1(:), v3(:) )
289  call vectr_dot ( ip, o(:), v1(:), o(:), xp(:) )
290 
291  if ( ip < -eps ) then ! right hand : exchange
292 ! write(ADM_LOG_FID,*) 'exchange by ip', i, '<->',j
293  vertex(i,:) = v2(:)
294  vertex(j,:) = v3(:)
295  endif
296 
297  enddo
298  enddo
299 
300  v1(:) = vertex(1,:)
301  v2(:) = vertex(2,:)
302  v3(:) = vertex(3,:)
303  ! if 1->2->3 is on the line
304  call vectr_cross( xp(:), v1(:), v2(:), v1(:), v3(:) )
305  call vectr_dot ( ip, o(:), v1(:), o(:), xp(:) )
306  call vectr_angle( angle1, v1(:), o, v2(:) )
307  call vectr_angle( angle2, v1(:), o, v3(:) )
308 ! write(ADM_LOG_FID,*) ip, angle1, angle2, abs(angle1)-abs(angle2)
309 
310  if ( abs(ip) < eps & ! on the same line
311  .AND. abs(angle2)-abs(angle1) < 0.0_rp ) then ! which is far?
312 ! write(ADM_LOG_FID,*) 'exchange by angle', 2, '<->', 3
313  vertex(2,:) = v3(:)
314  vertex(3,:) = v2(:)
315  endif
316 
317  v2(:) = vertex(nvert ,:)
318  v3(:) = vertex(nvert-1,:)
319  ! if 1->nvert->nvert-1 is on the line
320  call vectr_cross( xp(:), v1(:), v2(:), v1(:), v3(:) )
321  call vectr_dot ( ip, o(:), v1(:), o(:), xp(:) )
322  call vectr_angle( angle1, v1(:), o, v2(:) )
323  call vectr_angle( angle2, v1(:), o, v3(:) )
324 ! write(ADM_LOG_FID,*) ip, angle1, angle2, abs(angle1)-abs(angle2)
325 
326  if ( abs(ip) < eps & ! on the same line
327  .AND. abs(angle2)-abs(angle1) < 0.0_rp ) then ! which is far?
328 ! write(ADM_LOG_FID,*) 'exchange by angle', nvert, '<->', nvert-1
329  vertex(nvert, :) = v3(:)
330  vertex(nvert-1,:) = v2(:)
331  endif
332 
333  return
Here is the call graph for this function:

◆ vectr_triangle()

real(rp) function, public scale_vector::vectr_triangle ( real(rp), dimension(3), intent(in)  a,
real(rp), dimension(3), intent(in)  b,
real(rp), dimension(3), intent(in)  c,
character(len=*), intent(in)  polygon_type,
real(rp), intent(in)  radius 
)

Definition at line 342 of file scale_vector.F90.

References scale_const::const_eps, scale_const::const_pi, vectr_abs(), vectr_angle(), and vectr_cross().

342  use scale_const, only: &
343  const_eps, &
344  const_pi
345  implicit none
346 
347  real(RP), intent(in) :: a(3), b(3), c(3)
348  character(len=*), intent(in) :: polygon_type
349  real(RP), intent(in) :: radius
350  real(RP) :: area
351 
352  real(RP), parameter :: o(3) = 0.0_rp
353 
354  ! ON_PLANE
355  real(RP) :: abc(3)
356  real(RP) :: prd, r
357 
358  ! ON_SPHERE
359  real(RP) :: angle(3)
360  real(RP) :: oaob(3), oaoc(3)
361  real(RP) :: oboc(3), oboa(3)
362  real(RP) :: ocoa(3), ocob(3)
363  real(RP) :: abab, acac
364  real(RP) :: bcbc, baba
365  real(RP) :: caca, cbcb
366  !---------------------------------------------------------------------------
367 
368  area = 0.0_rp
369 
370  if ( polygon_type == 'ON_PLANE' ) then ! Note : On a plane, area = | ourter product of two vectors |.
371 
372  call vectr_cross( abc(:), a(:), b(:), a(:), c(:) )
373  call vectr_abs( prd, abc(:) )
374  call vectr_abs( r , a(:) )
375 
376  prd = 0.5_rp * prd !! triangle area
377  if ( r < const_eps * radius ) then
378  print *, "zero length?", a(:)
379  else
380  r = 1.0_rp / r !! 1 / length
381  endif
382 
383  area = prd * r*r * radius*radius
384 
385  elseif( polygon_type == 'ON_SPHERE' ) then ! On a unit sphere, area = sum of angles - pi.
386 
387  ! angle 1
388  call vectr_cross( oaob(:), o(:), a(:), o(:), b(:) )
389  call vectr_cross( oaoc(:), o(:), a(:), o(:), c(:) )
390  call vectr_abs( abab, oaob(:) )
391  call vectr_abs( acac, oaoc(:) )
392 
393  if ( abab < const_eps * radius .OR. acac < const_eps * radius ) then
394  !write(*,'(A,3(ES20.10))') "zero length abab or acac:", abab/radius, acac/radius
395  return
396  endif
397 
398  call vectr_angle( angle(1), oaob(:), o(:), oaoc(:) )
399 
400  ! angle 2
401  call vectr_cross( oboc(:), o(:), b(:), o(:), c(:) )
402  oboa(:) = -oaob(:)
403  call vectr_abs( bcbc, oboc(:) )
404  baba = abab
405 
406  if ( bcbc < const_eps * radius .OR. baba < const_eps * radius ) then
407  !write(*,'(A,3(ES20.10))') "zero length bcbc or baba:", bcbc/radius, baba/radius
408  return
409  endif
410 
411  call vectr_angle( angle(2), oboc(:), o(:), oboa(:) )
412 
413  ! angle 3
414  ocoa(:) = -oaoc(:)
415  ocob(:) = -oboc(:)
416  caca = acac
417  cbcb = bcbc
418 
419  if ( caca < const_eps * radius .OR. cbcb < const_eps * radius ) then
420  !write(*,'(A,3(ES20.10))') "zero length caca or cbcb:", caca/radius, cbcb/radius
421  return
422  endif
423 
424  call vectr_angle( angle(3), ocoa(:), o(:), ocob(:) )
425 
426  ! calc area
427  area = ( angle(1)+angle(2)+angle(3) - const_pi ) * radius*radius
428 
429  endif
430 
431  return
scale_const
module CONSTANT
Definition: scale_const.F90:14
scale_const::const_eps
real(rp), public const_eps
small number
Definition: scale_const.F90:36
scale_const::const_pi
real(rp), public const_pi
pi
Definition: scale_const.F90:34
Here is the call graph for this function:

◆ vectr_distance()

subroutine, public scale_vector::vectr_distance ( real(rp), intent(in)  r,
real(rp), intent(in)  lon1,
real(rp), intent(in)  lat1,
real(rp), intent(in)  lon2,
real(rp), intent(in)  lat2,
real(rp), intent(out)  dist 
)

Get horizontal distance on the sphere.

Definition at line 443 of file scale_vector.F90.

443  implicit none
444 
445  real(RP), intent(in) :: r ! radius in meter
446  real(RP), intent(in) :: lon1, lat1 ! in radian
447  real(RP), intent(in) :: lon2, lat2 ! in radian
448  real(RP), intent(out) :: dist ! distance of the two points in meter
449 
450  real(RP) :: gmm, gno_x, gno_y
451  !-----------------------------------------------------------------------
452 
453  gmm = sin(lat1) * sin(lat2) &
454  + cos(lat1) * cos(lat2) * cos(lon2-lon1)
455 
456  gno_x = gmm * ( cos(lat2) * sin(lon2-lon1) )
457  gno_y = gmm * ( cos(lat1) * sin(lat2) &
458  - sin(lat1) * cos(lat2) * cos(lon2-lon1) )
459 
460  dist = r * atan2( sqrt(gno_x*gno_x+gno_y*gno_y), gmm )
461 
462  return
Generated by   doxygen 1.8.13